This article explores the parallax method, providing a detailed example illustrating how trigonometry is employed in the mapping of our universe. It introduces the concept of stellar parallax, with a historical reference to Friedrich Wilhelm Bessel's measurement of 61 Cygni in 1838. Different types of parallax measurements are discussed, including ground-based parallax using optical and near-infrared observations, as well as space-based parallax observed by the Hubble Space Telescope. The use of Very Long Baseline Interferometry (VLBI) in radio astronomy is explained, highlighting its high precision in calculating the parallax of distant stars. The article concludes with insights into absolute and relative parallaxes, detailing the revolutionary Hipparcos satellite's absolute parallax determination and the advancements brought by ESA's Gaia satellite, which aims to create a precise 3-Dimensional map of over a billion stars in the Milky Way and beyond.

DIVING INTO THE MATTER
Introduction:
Have you ever wondered how we calculate the distance between stars that we see twinkle in the sky? Why are some of those stars bigger and farther away than others when they all look almost the same?
The answer to these questions is the use of the parallax method.
1. Parallax method
Parallax is the apparent shift or change in position of an object when viewed from different vantage points. A simple example of parallax is to hold your finger in front of your face and close one eye, then switch eyes. You'll notice your finger appears to shift against the background. This shift is due to the different lines of sight from each eye.
Similarly, in astronomy, parallax is used to measure the distance to stars. As Earth orbits the Sun, nearby stars appear to shift against the background of more distant stars. Astronomers observe this apparent change in position to calculate the distance to the star. The greater the shift, the closer the star is to Earth. It's like comparing the view of your finger from one eye to the view from the other eye, but on a cosmic scale.
Calculations
Let's understand this better with an example,
Suppose we want to find out the difference between Earth and a nearby star, as shown in the image below.
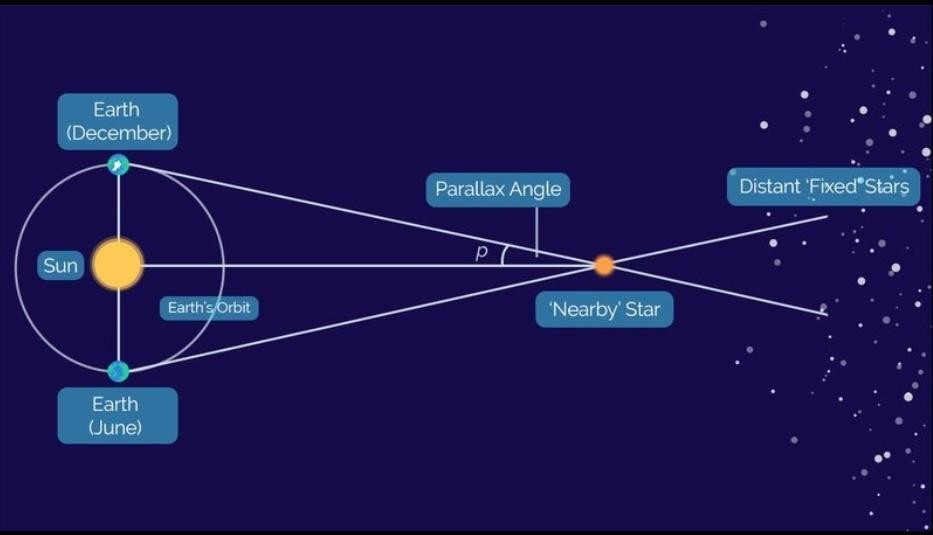
Figure 1.
The distance between the two points of observation is 2 an(Astronomical unit, is approximately the average distance between the Earth and the Sun which is equal to 150 million km or 8.3 light-minutes.) And the angle denoted by p is the parallax angle.
Using simple trigonometry we can deduce that,
The distance between Earth and the star if denoted by D can be given by,
D = 1AU/tan p
As p is going to be very small (usually measured in arcsec, 1/1000 of a degree; or mas, milliarcsecond )
Tan p ≈ p
Therefore we get,
D = 1AU/p
The distance measured is usually expressed in Parsec
1 Parsec = 1AU/1 arcsec
which is equal to 3.086*10^16m or 3.262 light years
2. Stellar parallax
German astronomer Friedrich Wilhelm Bessel was first to measure stellar parallax in 1838. He studied the tiny shift in the apparent position of a star called 61 Cygni (which is a binary star system in the constellation Cygnus) using the heliometer, designed by German physicist and lens maker Joseph von Fraunhofer.
He published the parallax of 61 Cygni as 0.314 arcsec, which is 10.3 light years.
Today's measurement of the same is 11.4 light years, that means Bessel’s calculations deviated only by about 10%, which was done in 1838. That is about a little less than two centuries back!
There are two major types of parallax we measure today,
2.1 Ground based Parallax
The history of stellar trigonometric parallax measurement highlights a slow start around 1900, with less than 100 stars having their parallaxes measured. Photographic techniques and systematic programs improved the situation, leading to 1682 stars with parallaxes in the 1924 General Catalogue. Subsequent editions increased the number to 6390, but precision remained modest. Significant advancements in the 1960s and 70s, using dedicated reflectors and automatic measuring engines, resulted in standard errors of 4 mas for fainter stars. The fourth edition of the General Catalogue in 1995 included parallaxes for 8112 stars, marking progress before the Hipparcos era.
2.1.1 Optical and near-infrared observations
The advent of CCDs (Charge coupled devices) and solid-state detectors in optical and near-infrared observations brought about a revolution in astrometry. These technologies, with improved positional stability and sensitivity, addressed issues that had long affected photographic astrometry, such as magnitude-dependent systematic errors. This transformation increased observation efficiency and expanded the accessibility of new object types, particularly ultracool stars in the solar neighbourhood. Parallax programs in recent decades have focused on nearby ultracool stars, providing a more comprehensive inventory. Optical wavelength programs at USNO, ESO/NTT, Torino, CTIO, and ESO, as well as near-infrared programs at ESO/NTT, USNO, CAHA, UKIRT, and CFHT, have achieved accuracies in the 1–5 mas range. Some programs, like those at USNO and CFHT, reach well below 1 mas, and a standard error of 0.3 mas is considered state-of-the-art at optical wavelengths.
2.1.2 Radio (VLBI)
Very Long Baseline Interferometry (VLBI) is a technique used in radio astronomy for high-resolution observations of celestial objects. It involves multiple radio telescopes spread over large geographic distances, sometimes spanning thousands of km. These telescopes operate together as a single virtual telescope through a process called interferometry.
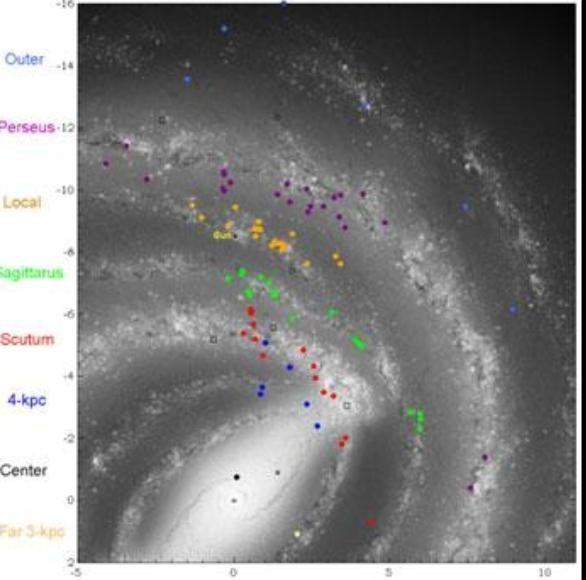
(Plan view of the Milky Way rotating clockwise.) ; Image credit: Annu. Rev. Astron. Astrophys. 2014. 54
In VLBI, signals received by each telescope are precisely time-stamped, and then the data from all telescopes are combined. This combination of signals allows astronomers to simulate a telescope with a size equal to the maximum separation between the individual telescopes, providing extremely high angular resolution, which is important while finding stellar parallax angle.
Very Long Baseline Interferometry (VLBI) can achieve high accuracy in calculating the parallax of distant stars. The theoretical precision of a single VLBI observation is on the order of 10 microarcseconds (µas). However, in practice, the precision is influenced by factors like path-length fluctuations in the ionosphere and troposphere.
The precision of a single observation is limited by how well these path-length fluctuations can be modelled or predicted. Residual errors are likely to be several centimetres, corresponding to an angular measurement precision of approximately 1 milliarcsecond (mas).

(Image of M33, a satellite of the Andromeda galaxy.The relative motion gives a "rotational parallax" distance.) ; Image credit:Annu. Rev. Astron. Astrophys. 2014. 54
To enhance accuracy, VLBI uses techniques like phase referencing, where the phase of the target source is observed differentially with respect to a radio-bright quasar. This method, if applied carefully and with stable reference sources, can directly yield the absolute parallax and proper motion of the target source. The precision achieved for certain radio-emitting stars, pulsars, and other celestial objects can be in the sub-milliarcsecond range or even better, making VLBI a powerful tool for astrometric measurements
2.2 Space based Parallax
In space, optical astrometric measurements benefit from the absence of atmospheric disturbances. The precision is theoretically limited by diffraction and photon noise. Using a telescope of approximately 1 metre in size, wide-band CCD detection, and a 1-minute exposure time, the limiting precision can reach about 5 microarcseconds for a V = 10 magnitude star.
The key challenges lie in providing a stable instrument and ensuring precise calibration. Weightlessness, a potentially stable thermal environment, and the ability to cover the entire celestial sphere with a single instrument contribute to improving the overall accuracy of space-based astrometric measurements.
2.2.1 Relative parallaxes: Hubble Space Telescope
Relative parallax refers to the measurement of the apparent shift or change in position of a celestial object compared to a nearby reference point. This reference point is often another star or a set of stars that are assumed to be at rest or to have a negligible parallax of their own.
The Fine Guidance Sensors (FGS) on the Hubble Space Telescope (HST) are two-axis shearing interferometers. One of them, FGS3 (and since 1999, FGS1r), is used for relative astrometry within a specific area. The astrometric calibration provides an accuracy of approximately 1 milliarcsecond (mas) per observation for stars in the magnitude range V = 3 to 17. The HST parallax program involves stars like Cepheids and RR Lyrae for calibrating period–luminosity relations, Hyades and Pleiades stars, and some fainter stars. The typical parallax accuracy achieved is in the range of 0.1–0.2 mas.
Image credit : Hubblesite

Image credit : Hubblesite
Due to the small field of the FGS and measurements being relative to reference stars with similar parallax factors, the obtained parallaxes are relative. A correction, typically 0.8–1.5 mas with an uncertainty of at least 10%, is added to account for the mean parallax of the reference stars.
However, relative parallax is more sensible than absolute parallax in expressing the stereoscopic effect.
2.2.2 Absolute parallaxes: Hipparcos and Gaia
Absolute parallax refers to the measurement of the apparent shift or change in position of a celestial object with respect to an observer on Earth, using a reference frame fixed in space. It provides the actual, intrinsic distance to the celestial object rather than a relative distance compared to another nearby object.
The Hipparcos satellite, launched in 1989, revolutionised absolute parallax determination with a unique technique involving large-angle optical measurements. It projected two widely separated fields in the same focal plane, enabling angular measurements between stars with different parallax factors (Fθ). By combining these measurements over time and varied geometric configurations, Hipparcos solved absolute parallaxes for all stars without prior assumptions. Despite controversy over the Hipparcos parallax zero point, particularly highlighted by Pleiades cluster data, global-scale tests, including ground-based parallaxes, HST/FGS results, orbital parallaxes for binaries, and distances from asteroseismology coupled with the infrared flux method, support the correctness of the zero point. The Pleiades cluster discrepancy remains a topic of ongoing discussion.
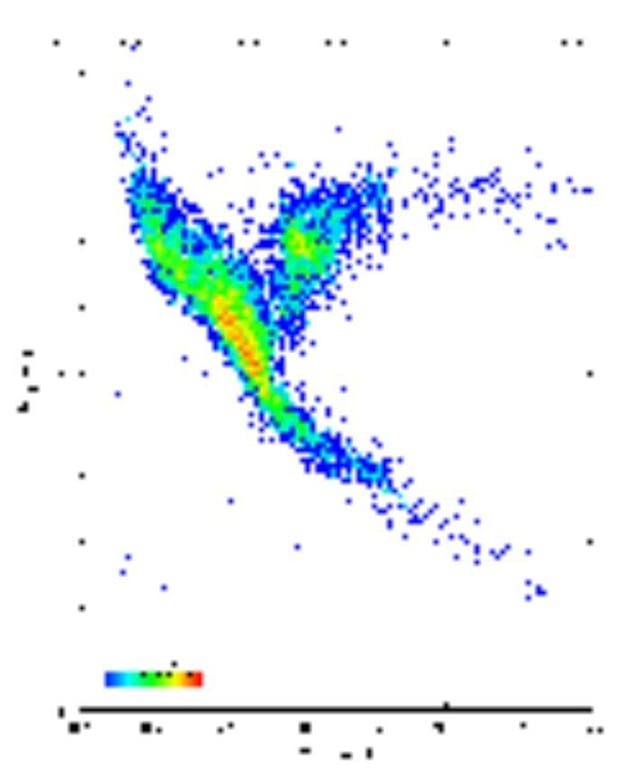
(Hertzsprung-Russell (M_Hp, V-I) diagram for the 41453 single stars from the Hipparcos Catalogue) ; Image credit: ESA
The Hipparcos Catalogue, published by ESA in 1997, provides parallaxes for approximately 118,000 stars, encompassing those brighter than a predefined limit (V ≃ 8 mag) and a selection of fainter stars. The typical standard errors for these parallaxes range from 0.8 to 2 milliarcseconds (mas).
ESA's Gaia satellite builds on the principles of Hipparcos but incorporates more efficient detectors (CCDs) and larger telescopes. Gaia is a groundbreaking mission aimed at constructing an exceptionally precise three-dimensional map of over a billion stars within the Milky Way galaxy and beyond.
Gaia's parallaxes are absolute, relying on a wide-angle measurement principle.To ensure accuracy, Gaia faces stringent demands on instrument stability, particularly the basic angle between its two viewing directions. Passive stabilisation guarantees a global parallax zero point error of less than 3.5 microarcseconds (µas). Additionally, the interferometric Basic Angle Monitor further reduces variations, minimising the zero point error to below 0.1 µas. This level of precision makes Gaia's parallaxes statistically meaningful even at extragalactic distances.
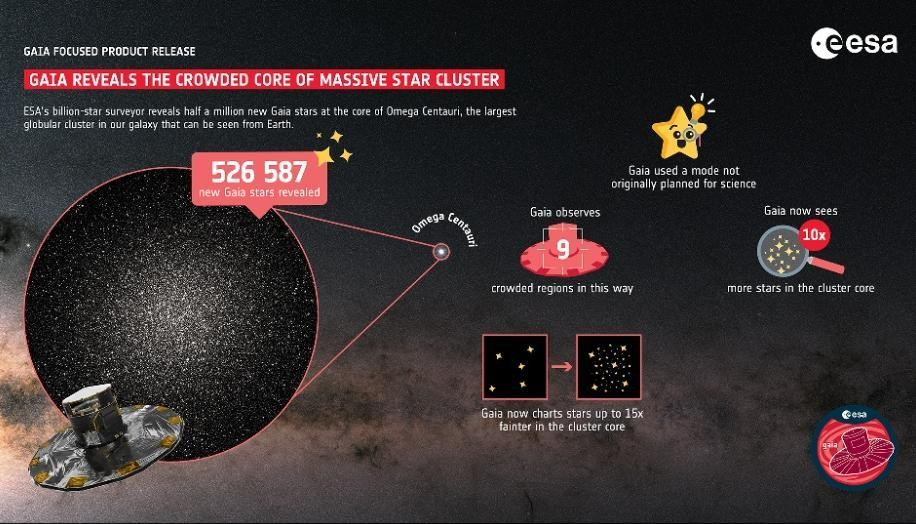
Image credit: ESA ; (On 10/10/2023, ESA's Gaia mission released a goldmine of knowledge about our galaxy and beyond.)
Conclusion:
We saw how we can calculate the distance of different celestial objects from the Earth and their diameter using simple trigonometry. With more precise instruments and methods such as radio (VLBI) and space based observations using telescopes like Hubble as well as satellites like Hipparcos and Gaia, whose accuracy is nearly 24 microseconds, we are able to make a 3D map of the universe that contains more than a billion stars and would cover about tens of thousands of light years from Earth. In conclusion, Gaia's recent successes highlight the continued importance of parallax in deepening our understanding of the vast universe. Parallax remains a crucial tool that propels our exploration of the cosmos.
References
Bessel, F. W. 1838, Astron. Nachr.
ESA 1997, The Hipparcos and Tycho Catalogues, ESA SP-1200
Bastian, U. & Hefele, H. 2005, in: The Three-Dimensional Universe with Gaia (Turon, C.,
O’Flaherty, K.S., & Perryman, M.A.C., eds.), ESA SP-576, p. 215
S¨oderhjelm, S. 2005, in: The Three-Dimensional Universe with Gaia (Turon, C., O’Flaherty,
K.S., & Perryman, M.A.C., eds.), ESA SP-576, p. 97
McArthur, B. E., Benedict, G. F., Harrison, T. E., & van Altena, W. 2011, AJ, 141, 172
Direct distance determination using parallax: Techniques, promises and limitations
Lennart Lindegren
THE HIPPARCOS CATALOGUES link
https://www.cosmos.esa.int/documents/532822/552851/vol6_all.pdf/5f8abb58-2bcb-4938-af70-4a197ccf59c4



