
Introduction
Precision measurement is a cornerstone of scientific research, enabling scientists and engineers to quantify the properties of matter and phenomena with high accuracy. The importance of precision lies in its ability to ensure reliable data, which is crucial for experiments, product development, and technological advancements. This article will explore the fundamental principles of measurement, historical developments, various types of measurements, the concept of measurement uncertainty, and their implications for future research.
Historical Context
The evolution of measurement techniques can be traced back to ancient civilizations, where rudimentary tools were used to quantify length, weight, and time. Over centuries, these techniques have advanced significantly, leading to the establishment of standardized measurement systems.
Key milestones in precision measurement include:
- The development of the metric system in the late 18th century, which aimed to provide a uniform system of measurements based on natural constants.
- The establishment of the International System of Units (SI) in the 20th century, providing a standardized framework for measurements in science and technology.
Types of Measurements
Measurements can be categorized into several types, each serving distinct purposes in scientific inquiry:
1. Length: Measured in meters (m), length measurement techniques include rulers, laser rangefinders, and interferometry.
2. Time: Measured in seconds (s), precision in time measurement has been enhanced by atomic clocks, which define the second based on the vibrations of cesium atoms.
3. Mass: Measured in kilograms (kg), mass measurements utilize balances and scales, ensuring consistency and precision.
The Role of Standards in Measurement
Standards play a vital role in ensuring that measurements are consistent and comparable across different laboratories and applications. The SI units serve as a global standard for measurements, facilitating communication and collaboration among scientists worldwide.
Measurement Uncertainty
Measurement uncertainty refers to the doubt that exists about the result of a measurement. It is a critical concept in precision measurement, as it quantifies the range within which the true value of the measured quantity is expected to lie.
Definition and Significance
Uncertainty is expressed as an interval around the measured value, providing a clear indication of the reliability of the measurement. For example, if a length is measured as "(10.0m-0.1m) to (10.0m+0.1m)", the true length is expected to lie between "9.9m, 10.0m, 10.1m"
Methods to Quantify Uncertainty
There are various methods to quantify uncertainty, including:
1. Type A Evaluation: Based on statistical analysis of repeated measurements. For instance, if multiple measurements of the same quantity yield values of "(10.0m-0.1m) to (10.0m+0.1m)", the mean can be calculated, and the standard deviation can be used to estimate uncertainty.
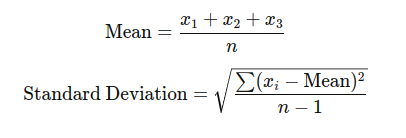
2. Type B Evaluation: Based on other sources of information, such as manufacturer specifications or published data.
Combining uncertainties from different sources is essential for providing a comprehensive measure of total uncertainty. This can be done using the root sum of squares method:
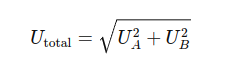
where Ua and Ub are the uncertainties from Type A and Type B evaluations, respectively.
Summary and Future Directions
In summary, precision measurement is fundamental to scientific research, evolving from basic techniques to sophisticated methods supported by international standards. Understanding the types of measurements and the concept of uncertainty allows researchers to quantify their findings effectively.
As technology advances, the need for enhanced precision and reliability in measurements will continue to grow, paving the way for new methodologies, especially in fields like quantum mechanics. The next article will delve into the role of quantum principles in advancing precision measurements, highlighting the intersection of these two critical areas of study.
Sample Questions
1. Question 1: A scientist measures the length of a rod multiple times, yielding the following values: 10.1m, 10.0m, 9.9m. Calculate the mean and standard deviation of the measurements.
2. Question 2: If a measurement of a physical quantity is reported as 50kg +-0.5kg, determine the range of values that represent the uncertainty in this measurement.
3. Question 3: An experiment reports the mass of a sample as 20.0g with Type A uncertainty of 0.2g and Type B uncertainty of 0.1g. Calculate the total uncertainty in the mass measurement.
These questions encourage the application of concepts discussed in the article and reinforce the understanding of precision measurement principles.



