The Raychaudhuri Equation, often referred to as the Landau–Raychaudhuri Equation, stands as a foundational pillar in the realm of general relativity. Developed independently by Amal Kumar Raychaudhuri and Lev Landau, this equation plays a pivotal role in understanding the motion of matter and the very fabric of spacetime. In this article, we embark on a journey to demystify this enigmatic equation and explore its profound implications in the field of physics.

Understanding the Background: Einstein's Field Equations of Gravitation (1915)
In order to truly grasp the significance of the Raychaudhuri Equation, it's crucial to delve into the historical context and the foundational work that led to its development. One of the key milestones in this journey was Albert Einstein's formulation of the Field Equations of Gravitation in 1915, which revolutionized our understanding of gravity and set the stage for the subsequent developments in the field of general relativity. [1]
Einstein's Pioneering Work:
In 1915, Albert Einstein presented a groundbreaking theory that would transform our comprehension of gravity. His theory, known as General Relativity (GR), represented a significant departure from Isaac Newton's classical theory of gravitation. While Newton described gravity as a force of attraction between masses, Einstein proposed an entirely new conceptual framework.
The Equivalence Principle:
At the heart of Einstein's theory was the equivalence principle, which posited that the effects of gravity were indistinguishable from the effects of acceleration. In simpler terms, if you were inside a sealed room with no windows and felt a force pushing you to the floor, you wouldn't be able to tell whether this force was due to gravity or the room accelerating upward. This principle challenged conventional notions of gravity as a force.
The Geometric Interpretation of Gravity:
Einstein's genius lay in his realization that gravity could be explained as the curvature of spacetime itself. According to his theory, massive objects, such as planets and stars, caused spacetime to curve around them. This curvature, in turn, influenced the motion of objects within the gravitational field. Instead of being attracted by a force, objects followed curved paths in a spacetime that had been bent by massive bodies.
Einstein's Field Equations:
Einstein's theory was encapsulated in his Field Equations of Gravitation, a set of mathematical equations that related the curvature of spacetime to the distribution of matter and energy. These equations, represented by tensor equations, became the cornerstone of GR. They can be expressed as:

Here, represents the Einstein tensor, which encapsulates the curvature of spacetime, is the energy-momentum tensor, describing the distribution of matter and energy, G is the gravitational constant, and c is the speed of light.
Key Takeaways:
Einstein's Field Equations marked a paradigm shift in our understanding of gravity:
Gravity was no longer a force but a result of spacetime curvature.
Mass and energy influenced the geometry of spacetime.
The equations predicted phenomena such as the bending of light by gravity, the precession of Mercury's orbit, and the existence of black holes.
Einstein's theory brought a new elegance and beauty to the description of the universe. However, it also posed new challenges, particularly regarding the behavior of matter and spacetime under extreme conditions, which ultimately led to the development of the Raychaudhuri Equation.
The Raychaudhuri Equation, as we shall see, plays a crucial role in understanding the consequences of Einstein's theory, especially concerning the formation of singularities and the nature of gravitational collapse. It emerged as a powerful tool in exploring the profound implications of GR, and its roots can be traced back to the mathematical and conceptual foundations laid down by Einstein over a century ago.
This historical context sets the stage for our exploration of the Raychaudhuri Equation and its significance in unraveling the mysteries of the cosmos.
Early Contributions from Indian Physicists:
To understand the historical significance of the Raychaudhuri Equation, we must explore the early contributions of Indian physicists in the field of general relativity. Two notable contributions that paved the way for later developments were made by Satyendranath Bose and Bibhutibhushan Datt.
1. Satyendranath Bose and Meghnad Saha (1920):
In 1920, Satyendranath Bose, in collaboration with Meghnad Saha, made a significant contribution by translating and disseminating the groundbreaking works of Albert Einstein and Hermann Minkowski on the theory of relativity. Their paper, titled "Einstein's Theory of Relativity (Translated)," was published in the "Bulletin of the Calcutta Mathematical Society." [2]
Key Highlights:
Dissemination of Einstein's Work: Bose and Saha played a pivotal role in introducing Albert Einstein's theory of relativity to the scientific community in India. They recognized the importance of this revolutionary theory and translated Einstein and Minkowski's papers into English, making them accessible to a broader audience.
Dissemination of Special and General Relativity: The translated papers included both special and general relativity, exposing Indian physicists to the concepts of spacetime curvature and the equivalence principle. This foundational knowledge was crucial for later developments in the field.
2. Bibhutibhushan Datt (1938):
In 1938, Bibhutibhushan Datt, a young physicist from Presidency College, Calcutta, made a notable contribution to the understanding of general relativity. His paper, titled "On the Field of a Single Centre in Einstein's Theory of Gravitation and the Motion of a Particle in that Field," was published in the "Proceedings of the Indian Academy of Sciences - Section A." [3]
Key Highlights:
Analysis of Einstein's Equations: Datt's work involved analyzing and partially solving the equations of general relativity, which described the gravitational field of a single central mass. This was an essential step in understanding how gravity behaves according to Einstein's theory.
Preceding Oppenheimer and Snyder: Notably, Datt's work preceded the analysis by Robert Oppenheimer and Hartland Snyder on gravitational collapse, which became a seminal paper in 1939. Datt's contributions laid the groundwork for future investigations into gravitational collapse.
These early contributions by Indian physicists, especially the dissemination of Einstein's theories and the analysis of gravitational fields, provided a solid foundation for the development of general relativity in India. They set the stage for subsequent research, including the work of Amalkumar Raychaudhuri, whose novel approach and development of the Raychaudhuri Equation further expanded our understanding of gravitational singularities and the nature of spacetime curvature. Raychaudhuri's equation, as we will explore, played a crucial role in proving singularity theorems and advancing our comprehension of the cosmos.
The Singular Challenge and Raychaudhuri’s Insight:
To delve deeper into the significance of the Raychaudhuri Equation, we need to understand the central challenge it aimed to address - the issue of singularities in the context of Einstein's theory of general relativity.
Singularities in Einstein's Equations:
When Albert Einstein formulated his theory of general relativity in 1915, it revolutionized our understanding of gravity. Instead of describing gravity as a force between masses, general relativity depicted it as the curvature of spacetime caused by mass and energy. This profound shift in our perspective on gravity introduced a new mathematical framework to describe the universe.
However, as physicists began to explore the consequences of Einstein's equations, they encountered a puzzling problem - singularities. Singularities are points in spacetime where the curvature becomes infinitely steep or the gravitational field becomes infinitely strong. These points represent locations where the usual laws of physics break down, making them a significant challenge to our understanding of the universe. [5], [6]
The Singularities Conundrum:
The early years of general relativity were marked by a struggle to comprehend why singularities occurred and what they truly meant. Singularities were problematic because they implied that Einstein's equations could lead to scenarios where spacetime itself became unpredictable and uncontrollable. Some of the questions that perplexed physicists included:
Nature of Singularities: What is the nature of these singularities? Are they real physical phenomena, or do they indicate a limitation of Einstein's theory?
Physical Significance: Do these singularities have physical significance, or are they simply mathematical artifacts that need to be removed or avoided?
Cosmological Implications: How do singularities affect our understanding of the universe's past and future? Could they provide insights into the Big Bang or the ultimate fate of the cosmos?
Amalkumar Raychaudhuri's Insight:
Amalkumar Raychaudhuri, a physicist in Calcutta in the early 1950s, embarked on a journey to unravel the mystery of singularities in general relativity. He approached this problem from a unique angle, departing from the focus on finding specific exact solutions of Einstein's equations, which had been the primary approach until then. [4]
Raychaudhuri's insight was to shift the perspective from analyzing the singularities of individual trajectories to understanding the behavior of a collection of trajectories, known as a congruence. Instead of looking at one particle's motion in isolation, he examined how multiple particles moved collectively through spacetime.
The Raychaudhuri Equation:
This novel perspective led to the development of the Raychaudhuri Equation, a fundamental equation in the study of spacetime dynamics. The Raychaudhuri Equation describes how the expansion of a congruence of trajectories changes as it moves through a curved spacetime. Mathematically, it takes the form:
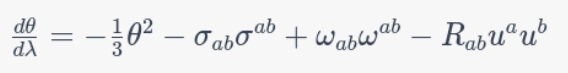
Expansion (θ): This term quantifies how the trajectories within the congruence diverge or converge.
Shear (σ_{ab}): Describes the stretching and squeezing of the trajectories.
Rotation (ω_{ab}): Represents the twisting or rotation of the trajectories.
Riemann Tensor (R_{ab}): Contains information about spacetime curvature.
Velocity (u^a): The velocity vector field along the trajectories.
Raychaudhuri's equation laid the groundwork for understanding the dynamics of spacetime curvature and the behavior of particles and light rays in gravitational fields. It provided a new way to approach the singularities problem by focusing on the properties of congruences and their evolution.
Singularities and the Raychaudhuri Equation:
The Raychaudhuri Equation played a pivotal role in addressing the singularities challenge. By analyzing the behavior of congruences and the factors that contribute to their expansion or contraction, physicists could gain insights into when and why singularities might occur in certain scenarios.
Moreover, the Raychaudhuri Equation became a fundamental tool in proving the singularity theorems of Roger Penrose and Stephen Hawking. These theorems demonstrated that, under specific conditions, singularities were not merely mathematical anomalies but inherent features of general relativity, signifying the limits of classical physics in extreme gravitational conditions.
Demystifying the Raychaudhuri Equation:
To truly understand the Raychaudhuri Equation, we need to unravel its intricacies and significance in the context of Einstein's theory of general relativity. Two key references, Amalkumar Raychaudhuri's 1955 paper titled "Relativistic cosmology. I" [4] and Sayan Kar's 2023 article "The what and the why of the Raychaudhuri equation," provide valuable insights into this fundamental equation. [7]
Amalkumar Raychaudhuri's 1955 Paper:
In his groundbreaking 1955 paper, Amalkumar Raychaudhuri introduced the Raychaudhuri Equation, a pivotal development in the study of spacetime dynamics and cosmology. This equation revolutionized our approach to understanding the behavior of matter and light in the presence of gravitational fields.
The Raychaudhuri Equation:
The Raychaudhuri Equation describes how the expansion of a congruence of trajectories evolves as it traverses a curved spacetime. In simple terms, it quantifies how bundles of geodesics (the paths that particles and light rays follow when they move freely through spacetime) either converge or diverge over time. The equation can be expressed as:
dθdλ=−13θ2−σabσab+ωabωab−Rabuaubdλdθ=−31θ2−σabσab+ωabωab−Rabuaub
Now, let's break down the key components of this equation:

Interpreting the Equation:
Now, let's decipher what this equation tells us:
The first term on the right-hand side (-1/3 θ^2) indicates that the expansion tends to decrease over time. In a universe dominated by attractive gravity (as we observe in our cosmos), particles tend to come closer together, leading to a convergence of trajectories.
The shear (σ_{ab}) term accounts for the stretching or squeezing of trajectories due to tidal gravitational forces. This term contributes to the overall behavior of the congruence.
The rotation (ω_{ab}) term represents the twisting or turning of the trajectories. In non-rotating systems, this term is typically zero.
The Riemann tensor (R_{ab}) encodes the curvature of spacetime caused by matter and energy. High curvature regions, such as those near massive objects, can significantly affect the trajectories.
The 4-velocity (u^a) terms connect the congruence's behavior to the distribution of mass and energy in spacetime.
Significance and Applications:
The Raychaudhuri Equation's significance extends far beyond cosmology. It plays a crucial role in understanding gravitational collapse, the behavior of black holes, and the singularity theorems formulated by Roger Penrose and Stephen Hawking. These theorems demonstrate that under certain conditions, singularities are inevitable outcomes of general relativity.
Sayan Kar's 2023 Article:
Sayan Kar's article, "The what and the why of the Raychaudhuri equation," [7] sheds light on the historical context and broader applications of the Raychaudhuri Equation. It emphasizes the equation's role in diverse fields, including optics, fluid dynamics, and quantum gravity.
Applications Beyond General Relativity:
The Raychaudhuri Equation, initially formulated within the realm of general relativity (GR), has found applications well beyond the theory of gravitation. Its versatility makes it a valuable tool in various branches of physics and astronomy. Let's explore some of its applications in cosmology, astronomy, and astrophysics:
1. Cosmology: In cosmology, the Raychaudhuri Equation plays a crucial role in understanding the large-scale dynamics of the universe. It helps cosmologists describe the expansion of the universe, including periods of acceleration and deceleration. By analyzing how the expansion rate (given by the Hubble parameter) changes over time, cosmologists can infer the properties of dark energy and dark matter, two mysterious components that dominate the universe's energy content.
2. Black Holes: The Raychaudhuri Equation is instrumental in studying black holes. It provides insights into the formation, growth, and behavior of black holes. For instance, it helps determine the event horizon, the point of no return beyond which nothing can escape a black hole's gravitational pull. The equation also plays a role in understanding the dynamics of matter falling into black holes and the formation of accretion disks.
3. Singularity Theorems: The Raychaudhuri Equation is a key ingredient in the singularity theorems developed by Roger Penrose and Stephen Hawking. These theorems demonstrate that, under certain conditions, spacetime singularities are inevitable outcomes of general relativity. Singularity theorems have profound implications for the fate of massive collapsing stars, the existence of singularities inside black holes, and the nature of the Big Bang singularity.
4. Gravitational Lensing: Gravitational lensing occurs when massive objects, such as galaxies or galaxy clusters, bend the path of light from more distant objects. The Raychaudhuri Equation helps astrophysicists predict and analyze the gravitational lensing effect. By studying how light rays converge or diverge in the presence of gravitational fields, astronomers can map the distribution of dark matter in the cosmos, probe the geometry of the universe, and detect distant galaxies and clusters.
5. Formation of Cosmic Structures: The Raychaudhuri Equation is involved in simulations of the large-scale structure of the universe. It helps model how galaxies, galaxy clusters, and cosmic filaments form and evolve under the influence of gravity. Understanding the growth of cosmic structures is essential for testing cosmological theories and comparing their predictions with observational data.
6. Optics and Beyond: Beyond astrophysics, the Raychaudhuri Equation has applications in optics, fluid dynamics, and even quantum gravity research. It offers a geometric perspective on the behavior of light rays in curved spacetime, making it relevant in the study of gravitational lensing in astrophysical observations. Additionally, researchers are exploring the possibility of formulating quantum versions of the Raychaudhuri Equation to deepen our understanding of the intersection between quantum mechanics and gravity.
Conclusion:
The Raychaudhuri Equation, originally conceived as a fundamental tool in Einstein's theory of general relativity, has transcended its origins to become a pivotal concept in the broader landscape of physics and astrophysics. Its significance lies in its capacity to elucidate the behavior of matter and light in gravitational fields and its far-reaching applications beyond the confines of general relativity.
From its early contributions to understanding the dynamics of the expanding universe to its central role in the formulation of singularity theorems, the Raychaudhuri Equation has left an indelible mark on cosmology and gravitational physics. It has enabled cosmologists to probe the mysteries of dark energy and dark matter, unravel the dynamics of cosmic expansion, and investigate the fundamental nature of spacetime singularities.
In the realm of black holes, the Raychaudhuri Equation has provided critical insights into the formation, structure, and accretion processes surrounding these enigmatic objects. It has also facilitated the study of gravitational lensing, allowing astronomers to map the distribution of dark matter, observe distant galaxies, and explore the geometry of the universe on cosmic scales.
Beyond its role in general relativity, the Raychaudhuri Equation has found applications in diverse fields, including optics, fluid dynamics, and quantum gravity research. Its geometric perspective on the convergence and divergence of trajectories has proven invaluable in understanding the behavior of light rays in curved spacetime.
As researchers continue to push the boundaries of our knowledge in cosmology, astrophysics, and beyond, the Raychaudhuri Equation remains an essential tool for unraveling the mysteries of the universe. Its adaptability and generality ensure that it will continue to play a prominent role in our quest to comprehend the fundamental forces and structures that govern the cosmos.
So, the Raychaudhuri Equation exemplifies the enduring impact of foundational concepts in physics. Its journey from a mathematical formulation in the early days of general relativity to its multifaceted applications in modern astrophysics exemplify the power of theoretical physics to illuminate the deepest aspects of our universe.
References:
Einstein, A. (1915). The Field Equations of Gravitation. Sitzungsberichte der Preussischen Akademie der Wissenschaften, 844-847.
Bose, S. N., & Saha, M. N. (1920). Einstein's Theory of Relativity (Translated). Bulletin of the Calcutta Mathematical Society, 12(2), 97-103.
Datt, B. (1938). On the Field of a Single Centre in Einstein's Theory of Gravitation and the Motion of a Particle in that Field. Proceedings of the Indian Academy of Sciences - Section A, 8(3), 225-226.
Raychaudhuri, A. (1955). Relativistic cosmology. I. Physical Review, 98(4), 1123-1126.
Penrose, R. (1965). "Gravitational collapse and space-time singularities." Phys. Rev. Lett., 14(3), 57-59.
Hawking, S. W., & Ellis, G. F. (1973). "The Large Scale Structure of Space-Time." Cambridge University Press.
Kar, S. (2023). The what and the why of the Raychaudhuri equation. Physics News, 50(4).



